Roof test - four meter truss


The truss to be constructed is for a roof which is 3 x 4 meters (9.8' x 13.1'). Eves will be 25 centimeters and the outside dimension of the building will be 2.5 x 3.5 meters (8.2' x 11.5'. Five trusses with a spacing of 62.5 centimeters are required (24.5"). Purlins attached under slope chord connect trusses and extend 25 centimeters beyound end walls to create end eves. This roof design will have added strength of surface deflection equal to bamboo thickness to purlins and slight sag between them.

Trigonometry is the relationship between the lengths of the different sides of triangles and the angles of triangles. There are books of tables which print the ratios of different sides and angles. One can also type the term describing the ratio into the google search box and hit enter/return and google will give the answer. 27.5 degrees is the selected angle because it is easy to set on my power saw. It's an angle I've grown accustomed to using, if you don't care about setting the angle on your saw, measure out what looks good to your eye.
The full width of the truss is four meters, thus, the distance to the center is 2 meters. To compute the height of the truss we need to know the length of the side opposite the roof angle of 27.5û. The ratio of the opposite side divided by the adjacent side of an angle is known as the "tangent." "h" in the drawing refers to the hypotenuse of the triangle which is half of the roof.
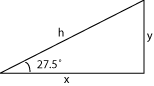
We are referring to the distance to the center as "x" (two meters) and we are solving for the height of the roof peak which is labeled "y." Without trigonometry tables we resort to the computer and type "tangent 27.5 degrees" in the google search box, hit return and the solution is rendered = 0.520567051. Two meters multiplied by 0.5206 is 1.04 meters, which is the height of the top of the truss.

This first truss was the only one made with small bent pieces at the peak. They were easily bent with heat but proved to be unnecessary.
The overall height of the truss is measured from the bottom of the horizontal length of bamboo to the top of the hypotenuse lengths which define the slope. Thus, because the bamboo is of various thicknesses, the center piece will vary in length (height).
